willcool4ever • 动态规划：“杨辉三角”

动态规划题目： “杨辉三角”不知道你听说过吗？我们现在对它进行一些改造。每个位置的数字可以随意填写，经过某个数字只能到达下面一层相邻的两个数字。设你站在第一层，往下移动，我们把移动到最底层所经过的所有数字之和，定义为路径的长度。请你编程求出从最高层移动到最底层的最短路径长度。

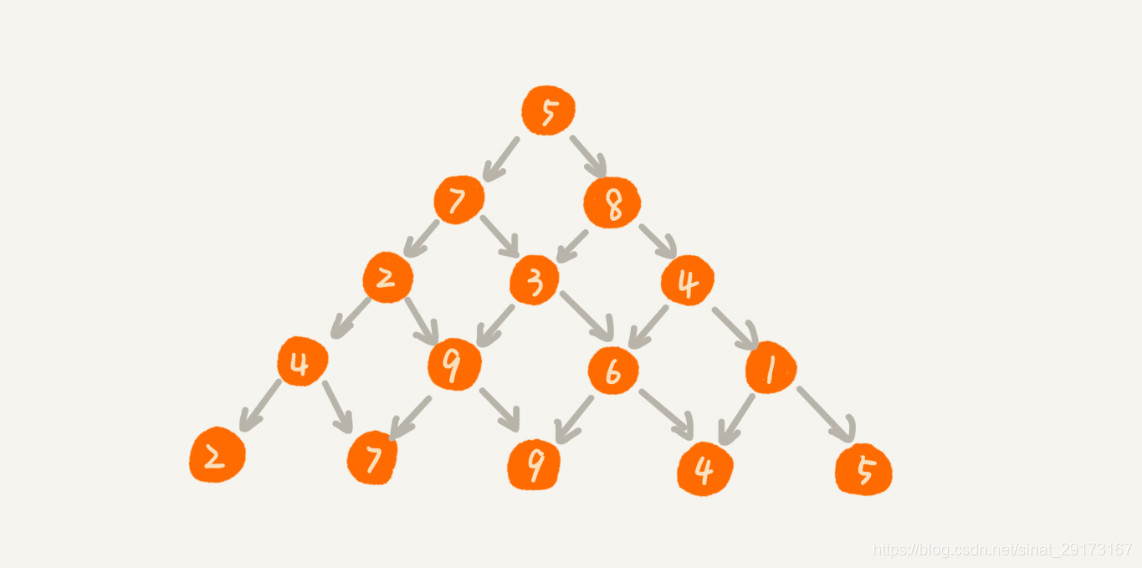
在这里插入图片描述

分析：

将题目中的“杨辉三角”放入矩阵中
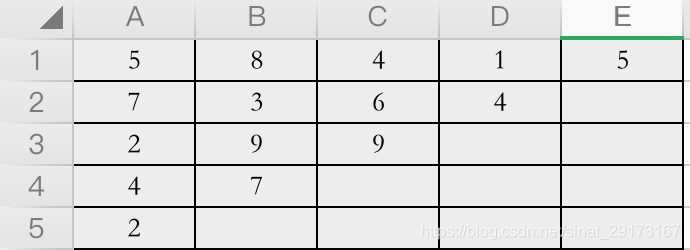
重新改写题目：从(1,A)开始的node，只能向右、向下移动，求到达边界时【边界：即过(5,A) 、(1,E）的直线】的最短路径【最短路径：路线上经过各点数的和最小】。
矩阵初始化，给边界求和
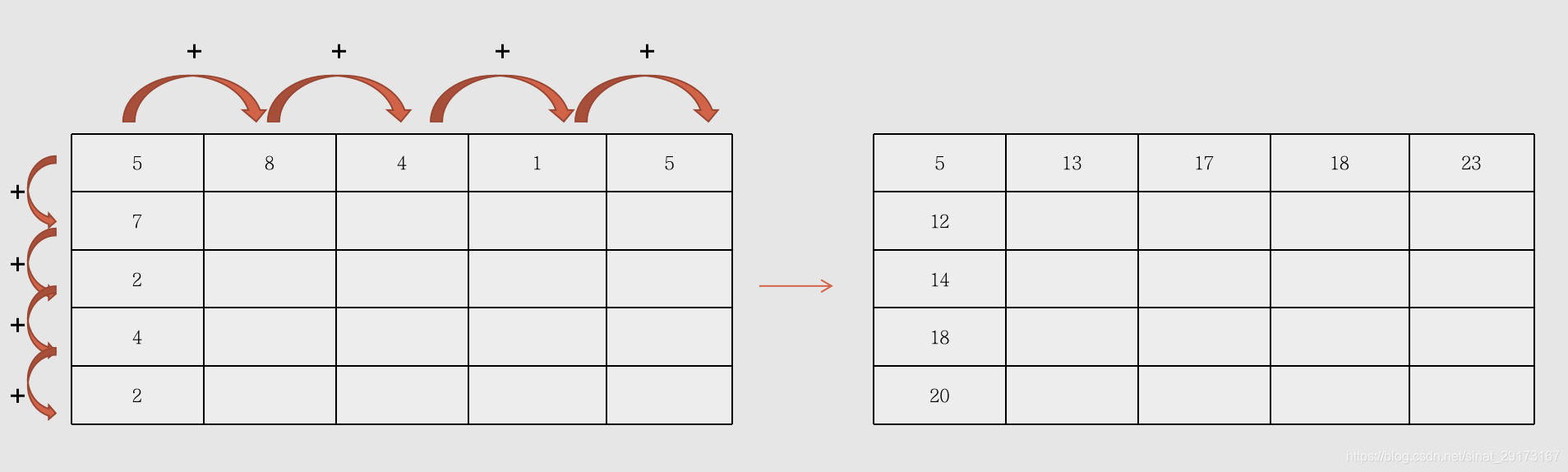
内部求值策略：当前值为选取两个方向：左侧、上方值的最小值，加上当前的路径值。[i,j] = [i,j] + min([i-1,j],[i,j-1])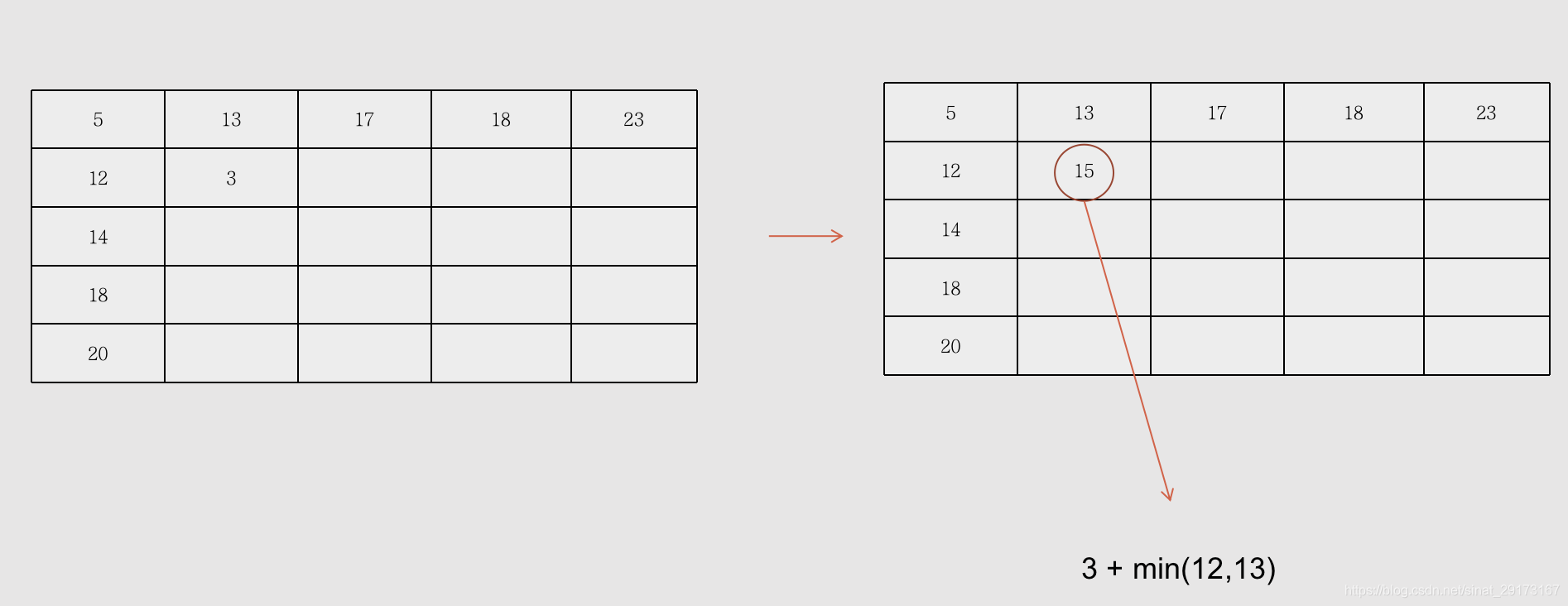
依次类推
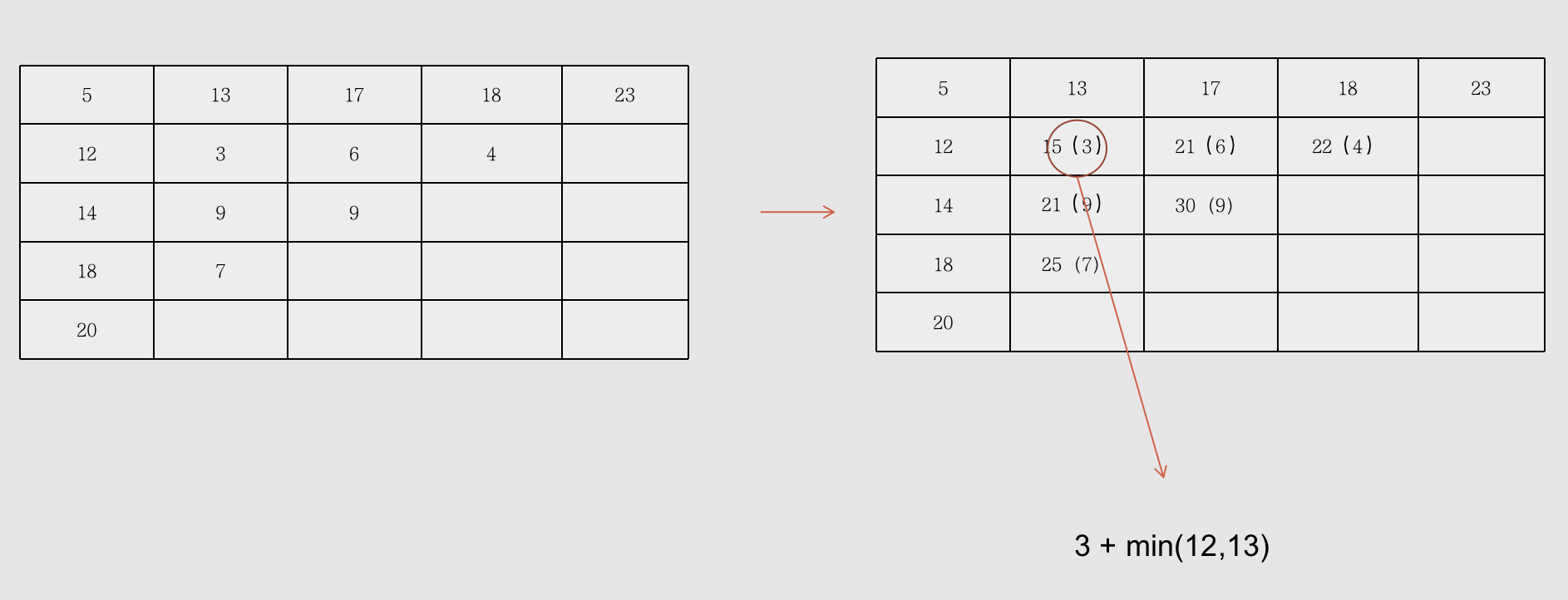
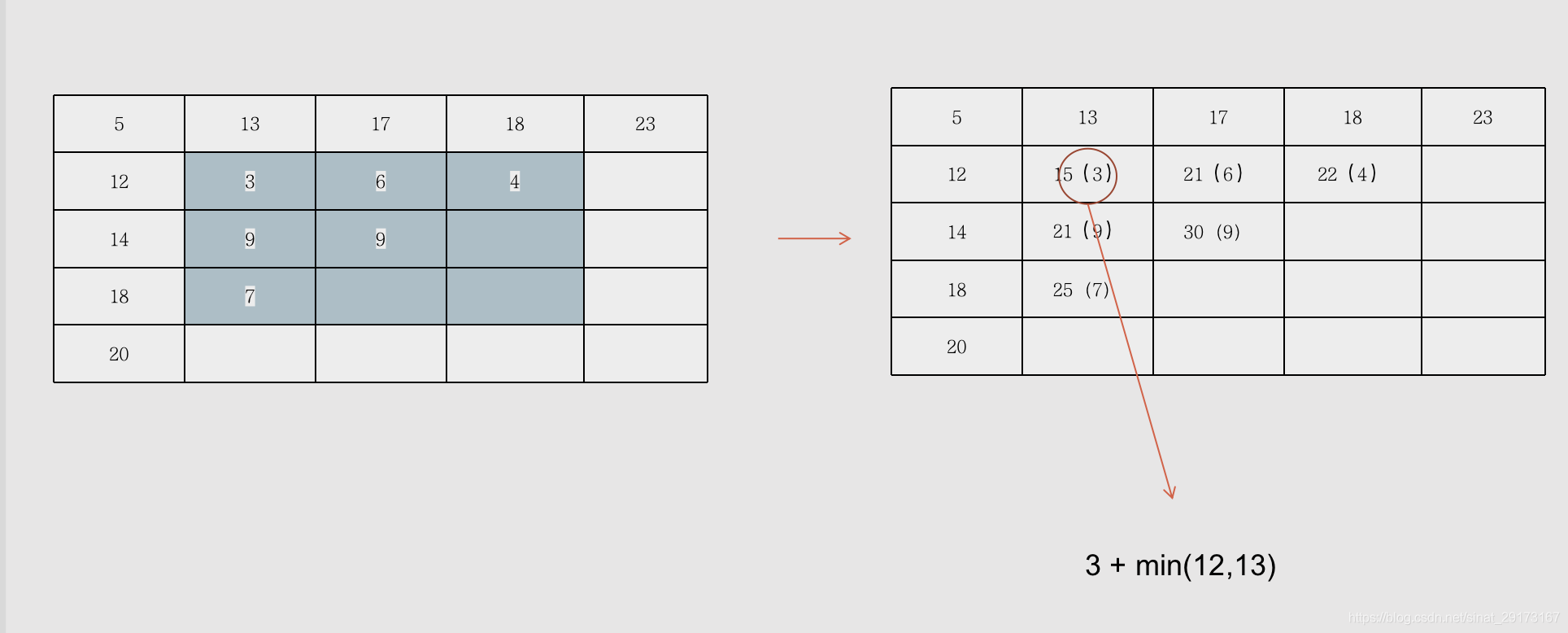
结论：最短路径为20
代码实现

// Example program
#include <iostream>
#include <vector>

using namespace std;

void print_m(int n, int (*matrix)[5])
{
    for (int i = 0; i < n; ++i)
    {

        for (int j = 0; j < n; ++j)
        {
            cout << matrix[i][j] << " ";
        }

        cout << endl;
    }

    cout << "~~~~~~~~~~~" << endl;
}

int main()
{

    int matrix[][5] = {{5, -1, -1, -1, -1}, {7, 8, -1, -1, -1}, {2, 3, 4, -1, -1}, {4, 9, 6, 1, -1}, {2, 7, 9, 4, 5}};
    print_m(5, matrix);

    // 整理数据
    for (size_t col = 0; col < 5; col++)
    {
        while (matrix[0][col] == -1)
        {
            for (size_t row = 1; row < 5; row++)
            {
                swap(matrix[row - 1][col], matrix[row][col]);
            }
        }
    }

    print_m(5, matrix);
    // 动态规划算法

    // step1 ：初始化0行
    for (size_t i = 1; i < 5; i++)
    {
        matrix[0][i] +=  matrix[0][i-1];
    }
    print_m(5, matrix);

    // step2 ：初始化0列
    for (size_t j = 1; j < 5; j++)
    {
        matrix[j][0] +=  matrix[j-1][0];
    }
    print_m(5, matrix);

    // step3: 计算内部的值
    for (size_t i = 1; i < 5; i++)
    {
        for (size_t j = 1; j < 5; j++)
        {
           matrix[i][j] += min<int>(matrix[i-1][j],matrix[i][j-1]);
        }
    }
    print_m(5, matrix);

    // step4：取边界上的最小值
    int idx = 4;
    vector<int> v;
    do
    {
      v.push_back(matrix[idx][4-idx]);

    } while (0<idx--);

    cout << "min path :" << min_element(v.begin(),v.end())[0] << endl;
}